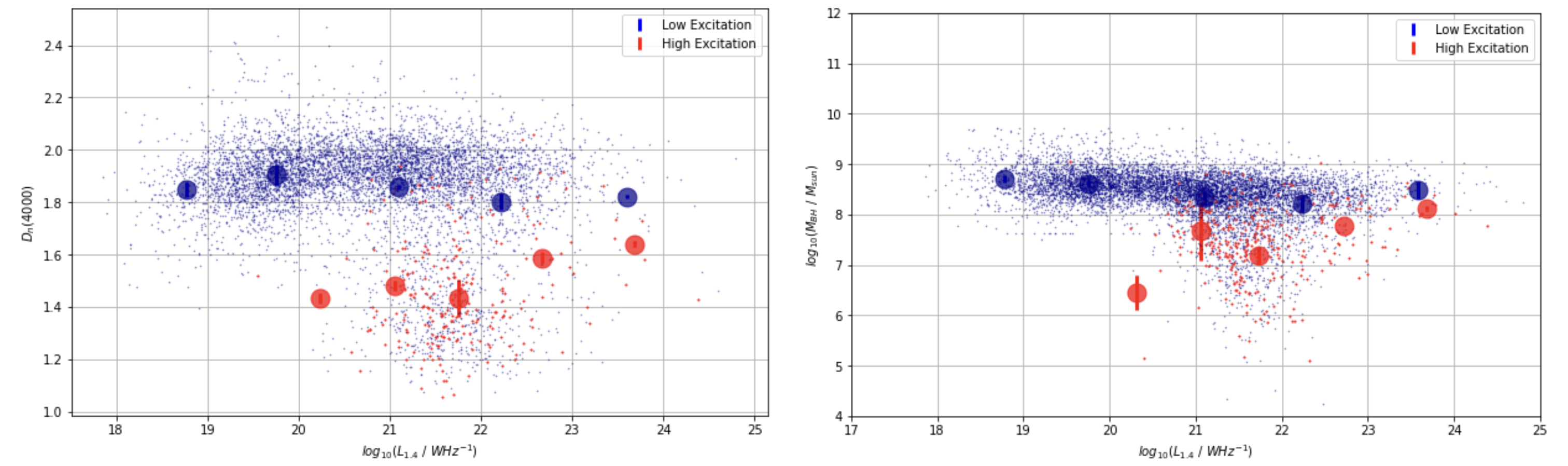
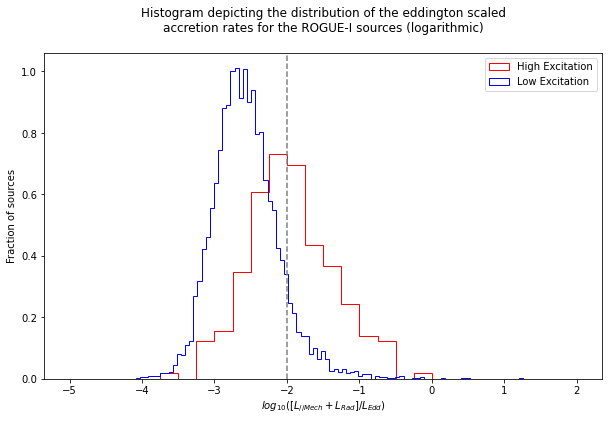
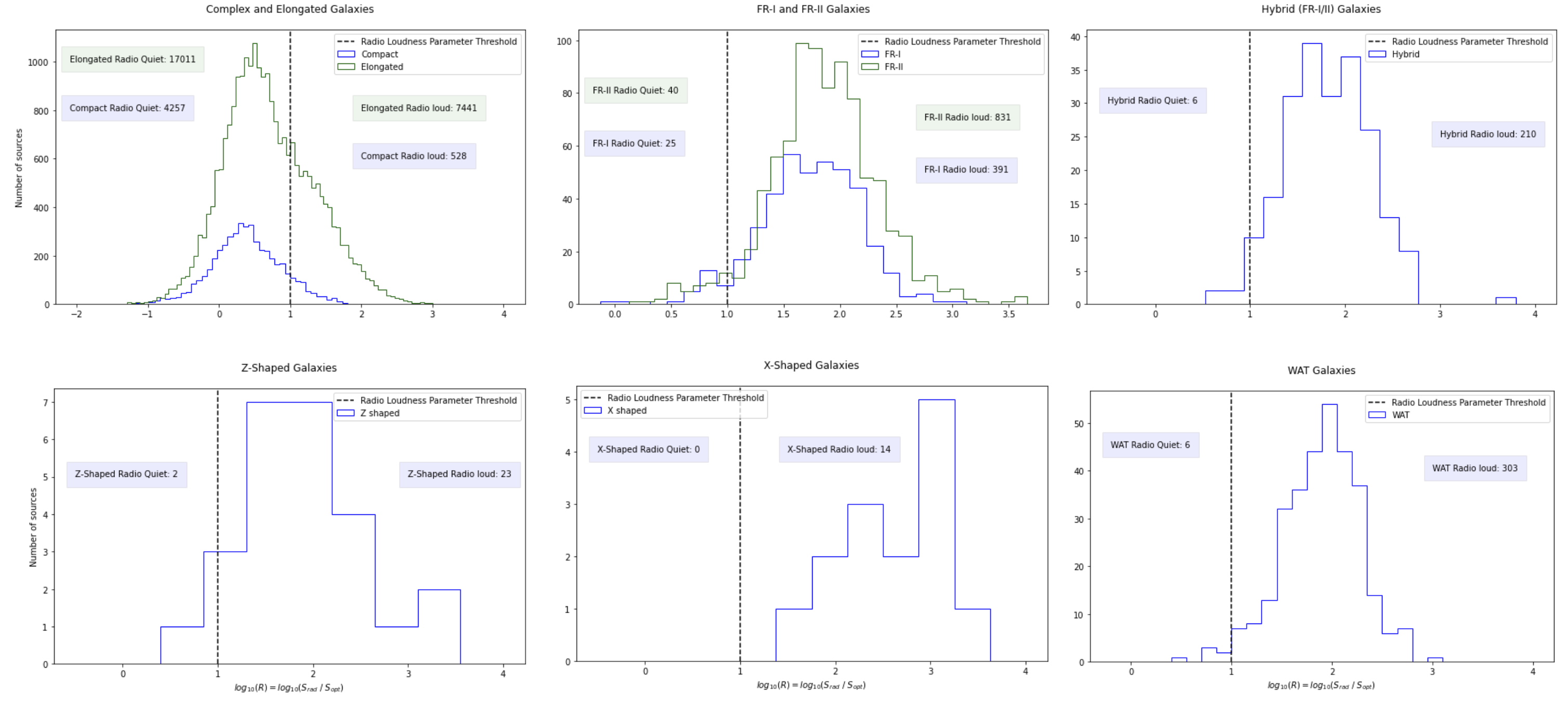
Overview:

This project explores whether the full spectral dimension of far-infrared and sub-millimeter emission lines—particularly multi-line, per-pixel spectra—can be used to infer spatially resolved galaxy properties at high redshift. Instead of relying on classical moment-0 (integrated flux) maps, the study leverages the complete velocity-channel structure of integral-field spectroscopic (IFU) data to predict key physical quantities: star-formation rate (SFR), molecular gas mass, stellar mass, gas temperature, and gas-phase metallicity. Synthetic IFU cubes generated from cosmological simulations and radiative-transfer modelling serve as the foundation for calibrating traditional flux–property relations and training machine-learning predictors that digest full spectral information.

Methodology

The project contrasts two complementary approaches:

• Classical Moment-0 Scaling: For each emission line, the velocity-integrated flux in each pixel is used to calibrate empirical relations mapping surface brightness to physical property surface densities. These relations approximate traditional extragalactic scaling laws.
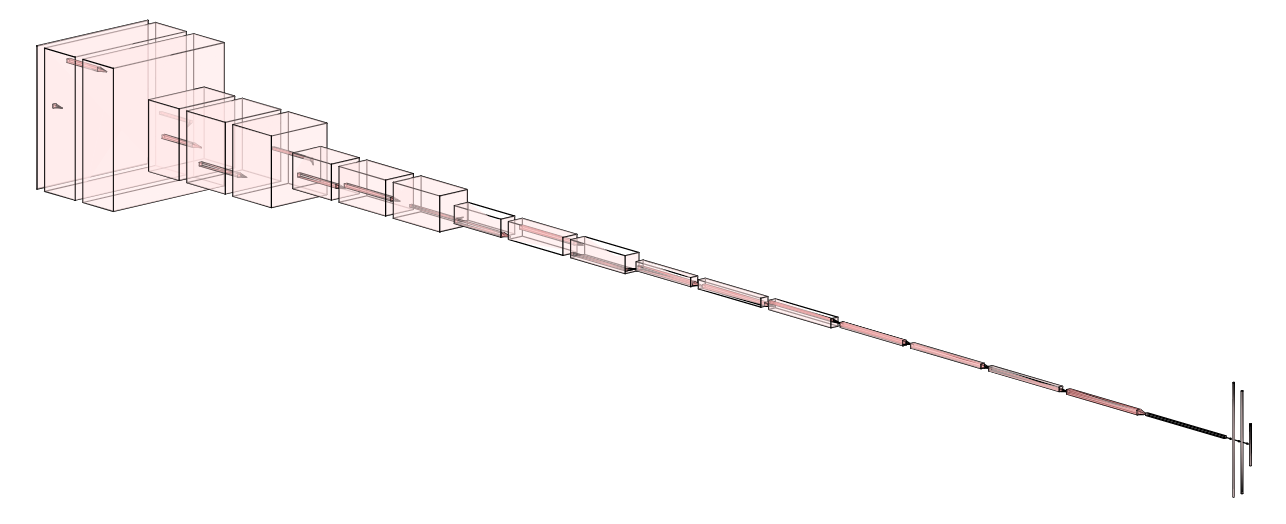
• Full-Spectrum Machine Learning: A supervised neural network ingests the per-pixel spectra of one or multiple emission lines. Convolutional layers act along the spectral axis to extract line-shape, width, asymmetry, and multi-line correlations, followed by dense layers that combine the learned features to predict the target physical property per pixel.
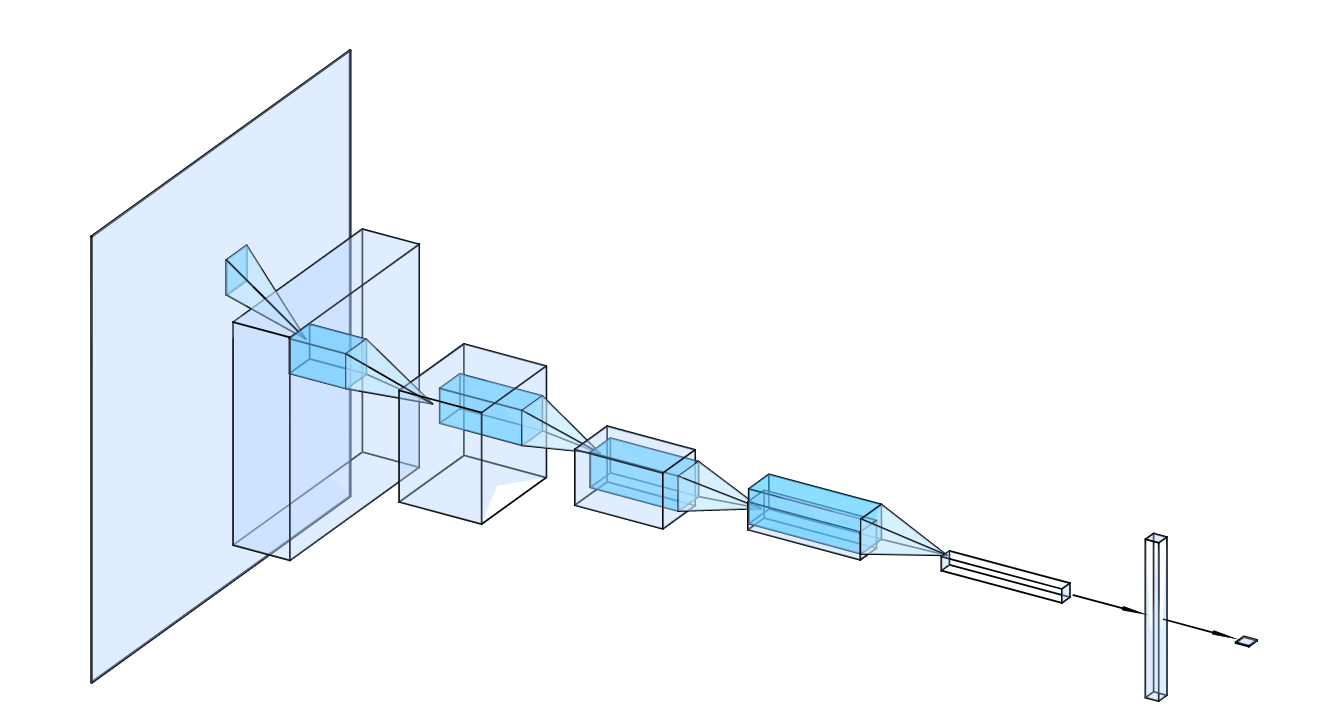
• Synthetic IFU Dataset: The input cubes are produced by applying radiative transfer and non-equilibrium chemistry to cosmological galaxy simulations. They span a broad range of redshifts, morphologies, inclinations, spatial resolutions, and dynamical states, ensuring a diverse and physically motivated training set.
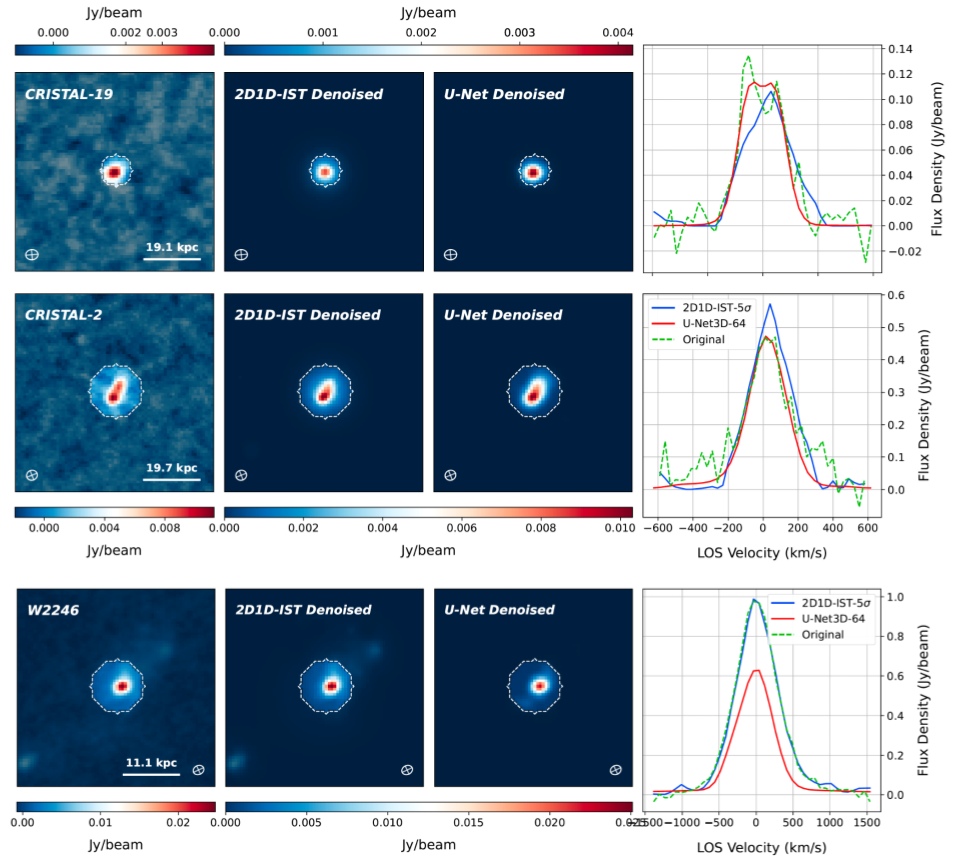
• Performance Evaluation: Predictions are compared against simulation ground truth through pixel-level residuals, scatter, bias, and morphology preservation across full 2D property maps.

Key Mathematical Framework

The classical method assumes that the relation between emission-line luminosity surface density and a given physical property follows a logarithmic form:

\[ \log \Sigma_{\mathrm{prop}} = a\,\log \Sigma_{\mathrm{line}} + b . \]

Here, \(\Sigma_{\mathrm{line}}\) is obtained by integrating the spectral flux density over all velocity channels:

\[ \Sigma_{\mathrm{line}} = \int I(v)\,dv . \]

To ensure physical consistency between simulated intensities and observational luminosity–property laws, solid-angle corrections, rest-frame frequencies, and pixel-area conversions are applied. This yields surface densities in \(\mathrm{kpc}^{-2}\) suitable for comparison to established observational relations.

The machine-learning model, in contrast, directly operates on the tensor of per-pixel spectra:

\[ X \in \mathbb{R}^{n_{\mathrm{lines}} \times N_{\mathrm{chan}}} , \]

applying convolutional kernels of shape \((1 \times 5)\) (for the multi-line case) to extract local spectral features across channels, followed by:

\[ \hat{y} = f_{\theta}(X) \]

where \(f_{\theta}\) is a nonlinear mapping encoded by the neural network parameters \(\theta\), producing the predicted physical property for that pixel.

Pipeline Summary

• Generate synthetic IFU cubes via radiative transfer applied to hydrodynamic simulations.
• Compute moment-0 maps and fit classical log–log relations to physical properties.
• Train and validate a spectral CNN on the full per-pixel line profiles.
• Compare predicted 2D property maps, residual distributions, and biases between methods.

Key Results & Insights

[ In Progress]

Overview:

This project benchmarks denoising strategies for three-dimensional spectral data cubes of high-redshift galaxies, spanning synthetic toy rotating-disk cubes, realistic mock IFU cubes from FIRE cosmological simulations, and ALMA observations (CRISTAL sample and W2246–0526). Methods compared include classical linear decompositions (PCA, ICA), sparse multiscale denoising (iterative 2D–1D wavelet soft-thresholding — IST), and a supervised 3D U-Net. Performance is assessed by RMSE, flux conservation within fixed emission apertures, preservation of spectral/spatial morphology, and SNR improvement.

Methodology

The experimental pipeline uses three classes of data (toy rotating-disk cubes, FIRE mock IFU cubes, ALMA CRISTAL & W2246) and four primary denoising strategies. The toy dataset is physically motivated (Sérsic radial profiles + vertical exponential, controlled inclination / rotation / beam convolution) and is used to train and evaluate supervised models.

• Data generation & pre-processing: Toy cubes are produced from a 3D flux density model combining a Sérsic radial profile and an exponential vertical profile; cubes are beam-convolved and injected with spatially correlated Gaussian noise at peak SNRs sampled between ~2.5–8.
• Unsupervised baselines: PCA and ICA on reshaped spectra (spaxel×channels) with component-selection guided by flux-plateau or explained-variance criteria; 2D–1D wavelet decomposition (Starlet 2D + 1D biorthogonal spectral wavelet) with iterative reweighted soft-thresholding (IST) for sparsity-driven denoising and a residual de-biasing step.
• Supervised method: A 3D U-Net (encoder–decoder with skip connections, average pooling to preserve flux, LeakyReLU activations) trained on 20,000 synthetic cubes (80/10/10 split) using an MSE loss and Adam optimizer. The architecture preserves spectral–spatial features and learns non-linear mappings to suppress noise.
• Evaluation & apertures: Fixed circular emission aperture defined observationally (aperture diameter $D_{ap} = 2\times\max(De, \mathrm{FWHM_{beam}})$ ) is used to compute total flux conservation and local RMSE within the aperture. Residual noise is estimated with MAD-based estimators to account for correlated noise.

Key Mathematical Framework

The toy spatial flux model uses a 3D Sérsic × exponential law:

where $R_e$ is the effective radius, $n$ the Sérsic index and $b_n$ the standard Sérsic constant (polynomial approx. for $n>0.36$):

References and derivation in the paper.

Denoising evaluation uses aperture total flux and RMSE within aperture:

Residual noise and SNR improvement are estimated using MAD-based noise estimates to handle beam-correlated noise.

Pipeline Steps (concise)

• Build / simulate toy cubes (Sérsic + kinematics + beam) and preprocess mock IFU/ALMA cubes.
• Train U-Net on synthetic cubes (20k examples).
• Apply PCA, ICA, IST, and U-Net to test / mock / real cubes (CRISTAL, W2246).
• Evaluate flux conservation, RMSE, spectral-shape preservation, and SNR improvement within fixed apertures.

Key Results & Insights

• Classical methods: PCA/ICA provide limited denoising in presence of spatially correlated (beam) noise; they struggle especially at low SNRs.
• Wavelet IST: Iterative 2D–1D soft-thresholding is physically interpretable and conserves flux well in medium-to-high peak SNR regimes (conserves >95% of aperture flux for CRISTAL; strong noise suppression), but tends to lose faint diffuse emission at very low SNR due to conservative thresholding.
• 3D U-Net: Trained on synthetic toy cubes, it generalizes strongly: lowest RMSE across tests, preserves spectral morphology (e.g., double-horned rotation signatures), and achieves the largest SNR improvements (factors ≈6–7 in CRISTAL examples). Caveats: slight flux overestimation / hallucinations at very low SNR and reduced recovery for morphologically very different diffuse systems (e.g., W2246 recovery ≈60%).
• Practical takeaway: A hybrid workflow — IST as an interpretable unsupervised baseline and a U-Net trained on broad synthetic priors (with transfer/fine-tuning on small real samples) — offers a robust route for denoising ALMA / IFU surveys.

Representative Numerical Highlights

• U-Net and IST both typically improve SNR by factors >6 for CRISTAL cubes; U-Net conserves >90% of aperture flux in CRISTAL, IST conserves >95% in high-SNR regimes.
• On W2246 (diffuse, turbulent system), IST conserves flux robustly and improves SNR by ≳2.5, while U-Net recovers ≈60% of aperture flux — illustrating limits of purely synthetic training for exotic real morphologies.

Conclusions & Future Directions

Deep supervised denoisers trained on well-designed, physically-motivated synthetic datasets generalize remarkably well to realistic IFU and ALMA data, offering substantial RMSE reduction and SNR gains. However, flux bias / hallucination risks at low SNR underline the need for uncertainty-aware models, hybrid architectures blending interpretable sparse priors with learned filters, and transfer learning to incorporate real-data priors (fine-tuning). The full paper outlines recommended next steps: uncertainty quantification, hybrid learnlet-like architectures, and incorporation of cosmological-simulation priors.

Overview:

This project investigates the interpretability of Convolutional Neural Networks (CNNs) applied to field-level cosmological inference. Utilizing the CAMELS (Cosmology and Astrophysics with MachinE Learning Simulations) dataset, specifically the IllustrisTNG suite, this work explores how neural networks extract cosmological parameters ($\Omega_m$ and $\sigma_8$) from total matter density fields in the presence of complex baryonic physics. The study focuses on identifying which morphological features of the cosmic web—such as voids, filaments, or halos—drive the network's predictions.

Methodology

The analysis pipeline consists of three primary stages:

• Simulation-Based Inference: A CNN is trained to map 2D total matter density fields ($X$) to the posterior distributions of cosmological parameters ($\theta$), predicting both the mean and variance. The networks are trained on fields from the CAMELS-TNG suite and evaluated on CAMELS-SIMBA to test robustness against baryonic feedback models.
• Attribution Mapping: Post-training, interpretability algorithms, including Saliency Maps, Integrated Gradients, and GradientSHAP, are applied to quantify the contribution of individual pixels to the model's inference. Integrated Gradients was selected as the primary method due to its adherence to axioms like sensitivity and implementation invariance.
• Information Cutting: The robustness of the model is tested by systematically removing information via Fourier scale cuts ($k_{max}$) and density threshold cuts ($\rho_{min}, \rho_{max}$). This involves retraining the networks on modified fields where certain scales or density regimes are filtered out to assess information content.

Key Mathematical Framework

The neural network predicts the mean ($\mu_i$) and variance ($\sigma_i^2$) of the marginal posterior for the $i$-th parameter:

$$ \mu_{i}(X)=\int_{\theta_{i}}p(\theta_{i}|X)\theta_{i}d\theta_{i} $$ $$ \sigma_{i}^{2}(X)=\int_{\theta_{i}}p(\theta_{i}|X)(\theta_{i}-\mu_{i})^{2}d\theta_{i} $$

To optimize these predictions, the model minimizes a custom loss function designed for moment matching, assuming the posterior can be approximated by a Gaussian:

$$ \begin{aligned} \mathcal{L} &= \sum_{i=1}^{6}\log\left(\sum_{j\in \mathrm{batch}}(\theta_{i,j}-\mu_{i,j})^{2}\right) \\ &\quad+ \sum_{i=1}^{6}\log\left(\sum_{j\in \mathrm{batch}}\big( (\theta_{i,j}-\mu_{i,j})^{2}-\sigma_{i,j}^{2} \big)^{2}\right) \end{aligned} $$

To interpret how the model learns, the Integrated Gradients (IG) method was chosen for its mathematical robustness. IG calculates the path integral of the gradients from a baseline input $x'$ (noise) to the actual input $x$:

$$ IG_{i}(x)=(x_{i}-x_{i}^{\prime})\int_{0}^{1}\frac{\partial f(x^{\prime}+\alpha(x-x^{\prime}))}{\partial x_{i}}d\alpha $$

Key Results & Insights

• Morphological Focus: Attribution maps reveal that CNNs extract cosmological information from both high-density regions (halos) and low-density regions (voids). While overdense regions provide the most "information per pixel," underdense regions contribute significantly due to their large spatial extent and coherent features.
• Robustness to Scale Cuts: The model demonstrates remarkable robustness to Fourier scale cuts. There is negligible degradation in cosmological constraining power even after removing small scales (cutting at $k_{max} \sim 20~h/Mpc$), suggesting the network can marginalize over uncertain baryonic effects that dominate small scales.



• Baryonic Independence: Experiments comparing full hydrodynamic simulations to gravity-only (N-body) simulations yielded similar results for $\Omega_m$, implying the neural network effectively learns the underlying dark matter morphology regardless of baryonic feedback mechanisms.
• The Power of Voids: Density cut analysis showed that even when high-density halos are removed, the network retains significant accuracy by relying on the structures within voids and filaments.



• Scale Cut Impact: Training models with a smoothing scale of $k_{max} = 1~h/Mpc$ resulted in a significant loss of constraining power for $\Omega_m$ and $\sigma_8$, indicating that information on scales smaller than $1~h/Mpc$ is critical for optimal parameter inference.

Overview:

This project involves training convolutional neural networks to infer a single cosmological parameter A from analytically generated 2D Gaussian density field (GDF) maps. Maps are realizations of a known power spectrum \(\,P(k)=A/k\,\). The aim is to test whether CNNs can extract essentially all information available in Gaussian fields, i.e., whether their predictive uncertainty approaches the theoretical Cramér–Rao / Fisher information bound.

Data Generation & Pre-processing

• Power spectrum: \(P(k)=\dfrac{A}{k}\), with \(A\) the only free parameter.
• Parameter sampling: \(A\sim\mathcal{N}(1.0,\,\sigma=0.2)\), clipped to the interval \([0.8,\,1.2]\).
• Map generation: 100,000 independent Gaussian density-field realizations of size \(64\times64\) pixels generated with the Pylians library (Fourier-space sampling consistent with \(P(k)\)).
• Normalization: Maps are z-score normalized (dataset mean and standard deviation). Parameter \(A\) is min-max scaled to \([0,1]\).
• Dataset split: 70% training, 15% validation, 15% test.

CNN Architecture & Training

• Framework: PyTorch.
• Architecture: 5 convolutional layers (kernel size 4, stride 2, padding 1) with LeakyReLU (α=0.2), followed by flatten → fully connected head → single regression output predicting \(A\).
• Loss: Mean Squared Error (MSE): \[ L = \frac{1}{N}\sum_{i=1}^{N}(A_{\text{true},i}-A_{\text{NN},i})^2 . \]
• Optimizer & regularization: Adam optimizer with weight decay; no dropout used.
• Hyperparameter search: Optuna (TPE sampler), tuning learning rate, weight decay, and number of filters. 50 trials; each trial trained up to 200 epochs.

Theoretical Validation — Fisher Matrix

For the single-parameter model \(P(k)=A/k\), the Fisher information for Gaussian fields (counting independent Fourier modes) simplifies to:

\[ F = \frac{N_{\mathrm{modes}}}{2A^2}, \qquad \sigma(A)_{\mathrm{Fisher}} = A\sqrt{\frac{2}{N_{\mathrm{modes}}}} . \]

Averaging over the allowed parameter interval \([A_{\min},A_{\max}]=[0.8,1.2]\) yields the mean expected error:

\[ \langle \sigma(A)\rangle = \sqrt{ \frac{A_{\min}^2 + A_{\min}A_{\max} + A_{\max}^2}{1.5\,N_{\mathrm{modes}}} }. \]

The empirical CNN error is then compared to this theoretical bound: if close, the network is effectively extracting nearly all available information from the Gaussian maps.

Experiments

1. Baseline — Original Gaussian Maps

• Train CNN on raw \(64\times64\) maps and evaluate predictive scatter on held-out tests.
• Create extra evaluation sets (20,000 samples each) at fixed \(A = 0.82,\ 1.00,\ 1.18\) to study conditional prediction spread and calibration.
• Compare empirical \(\sigma_A\) to Fisher-predicted \(\sigma(A)\) for the full \(k\)-range of the maps.

2. Fourier-Filtered Maps (Top-Hat Filters)

• Apply sharp Fourier-space cutoffs with \(k_{\max}=0.2,\ 0.15,\ 0.1\) (and \(k_{\min}=0\)).
• Retrain the CNN per filter scale and recompute empirical \(\sigma_A\).
• Compute \(N_{\mathrm{modes}}\) for each \(k_{\max}\) and compare Fisher bound to network error.

3. Gaussian-Smoothed Maps

• Apply Gaussian smoothing kernels (width = 1 px and 2 px) in image space; retrain for each smoothing level.
• Because analytic Fisher bounds are not directly available for smoothed maps, infer an effective \(N_{\mathrm{modes}}\) from the measured \(\sigma_A\) using:

\[ N_{\mathrm{modes}} = \frac{A_{\min}^2 + A_{\min}A_{\max} + A_{\max}^2}{\sigma_A^2}. \]

Implementation Details

• Language: Python 3
• Key libraries: PyTorch · NumPy · Matplotlib · Pylians · Optuna
• Hardware: GPU recommended (CUDA) for training efficiency
• Metrics: MSE; scatter plots of predicted vs true A; conditional prediction distributions at fixed A

Outcomes & Insights

• The CNN achieves parameter-estimation precision close to the Fisher-limit for the original (full-k) Gaussian maps, indicating that the network extracts nearly all available information from the fields.
• Reducing \(k_{\max}\) (via top-hat filtering) or increasing smoothing reduces the number of accessible Fourier modes, increasing the Fisher bound and the observed CNN error; the network errors track the theoretical expectations.
• By interpreting empirical errors in terms of an effective \(N_{\mathrm{modes}}\), smoothed maps can be assigned an equivalent information content consistent with the degradation due to smoothing.
• Overall conclusion: deep CNNs can act as near-optimal information extractors for Gaussian random fields when trained on sufficiently large datasets with architectures that capture relevant Fourier-domain structure.

Overview:

This project presents a comprehensive analysis of Active Galactic Nuclei (AGN) properties, focusing on the interplay between optical spectral classification, accretion efficiency, and radio jet production. By integrating data from radio (1.4 GHz) and optical (R-band, emission lines) surveys, the study characterizes the fundamental dichotomy between High-Excitation (HERG) and Low-Excitation (LERG) radio galaxies and explores how these classes map onto the fundamental plane of black hole activity. The analysis culminates in a rigorous classification of Radio Loud (RL) and Radio Quiet (RQ) sources using both core and total flux measurements.

Methodology & Mathematical Framework

The analysis pipeline is structured into three sequential modules, each building upon the physical properties derived in the previous steps:

1. HERG and LERG Dichotomy

The first stage classifies AGN based on the ionization state of their narrow-line regions. Sources are divided into High-Excitation Radio Galaxies (HERGs) and Low-Excitation Radio Galaxies (LERGs) using an Excitation Index (EI) derived from key optical emission line ratios (e.g., [OIII]/Hβ, [NII]/Hα).

• Classification Criterion: Sources with \( EI > 0.95 \) are classified as HERGs (indicating radiatively efficient accretion), while those below are LERGs (indicating radiatively inefficient, advection-dominated flows).
• Property Analysis: The study correlates this classification with physical host galaxy properties, including the \( D_n(4000) \) break (stellar age proxy), concentration index \( R_{90}/R_{50} \), and black hole mass \( M_{BH} \).

2. Eddington Scaled Accretion Rate

To understand the physical driver behind the HERG/LERG dichotomy, the project calculates the Eddington-scaled accretion rate (\( \lambda \)). This metric quantifies the accretion efficiency by comparing the total bolometric luminosity to the theoretical Eddington limit.

The total energy output is modeled as the sum of radiative (\( L_{rad} \)) and mechanical (\( L_{mech} \)) components:

$$ L_{rad} = 3500 \times L_{[\text{OIII}]} $$ $$ L_{mech} = 7.3 \times 10^{36} \times \left( \frac{L_{1.4\text{GHz}}}{10^{24} \text{ W Hz}^{-1}} \right)^{0.7} \text{ [erg s}^{-1}\text{]} $$

The dimensionless accretion rate is then defined as:

$$ \lambda = \frac{L_{bol}}{L_{Edd}} = \frac{L_{rad} + L_{mech}}{1.26 \times 10^{38} (M_{BH}/M_{\odot})} $$

3. Radio Loud (RL) and Radio Quiet (RQ) Classification

The final phase categorizes sources based on their radio-to-optical flux ratio. This analysis was performed twice to assess the impact of resolution effects: once using Total Radio Flux and again using Core Radio Flux.

The radio loudness parameter \( R \) is calculated in logarithmic space:

$$ R = \log\left( \frac{F_{1.4\text{GHz}}}{F_{R\text{-band}}} \right) $$

A threshold of \( \log(R) > 1 \) is utilized to define Radio Loud galaxies, distinguishing jet-dominated systems from those where radio emission may be dominated by star formation.

Key Results & Insights

• Accretion Modes: The accretion rate analysis confirms a physical distinction between the classes. HERGs typically exhibit high excitation rates (\( \log \lambda \gtrsim -2 \)) consistent with standard thin accretion disks, while LERGs populate the low-accretion regime (\( \log \lambda \lesssim -2 \)), powered by advection-dominated accretion flows (ADAFs).
• Energetic Output: The inclusion of \( L_{mech} \) in the bolometric luminosity calculation highlights that for many LERGs, the primary energy output is kinetic (jets) rather than radiative, a crucial correction often missed in optical-only studies.
• Morphological Connections: The RL/RQ classification reveals that radio loudness is not strictly binary but forms a continuous distribution. However, using core flux provides a sharper distinction for jet-dominated AGN compared to total flux, which can be contaminated by extended lobe emissions.

Overview:

This project implements a multi-phase photometric pipeline to identify and classify Young Stellar Objects (YSOs) within a star-forming region. Utilizing multi-wavelength data from Spitzer/IRAC (mid-infrared), 2MASS (near-infrared), and Herschel (column density maps), the study aims to distinguish true protostars from extragalactic contaminants. The analysis is split into two phases: an initial classification based on infrared colors, followed by a rigorous extinction correction process to account for interstellar reddening caused by dust, thereby refining the separation between Class I (protostars) and Class II (pre-main sequence stars with disks) objects.

Methodology

The classification pipeline consists of four primary stages:

• Data Filtering & Quality Control: The raw Spitzer catalog is filtered to retain only sources with photometric uncertainties $\sigma < 0.2$ mag in all four IRAC bands ($3.6, 4.5, 5.8, 8.0 \mu m$).
• Contaminant Removal: Specific color-color and color-magnitude cuts are applied to remove extragalactic contaminants, including star-forming PAH galaxies, Active Galactic Nuclei (AGN), and shock emissions.
• Phase 1 Classification: Remaining sources are classified into Class I and Class II YSOs based on their mid-infrared spectral indices derived from IRAC color spaces.
• Phase 2 Extinction Correction: Sources are cross-matched with 2MASS and Herschel data. Visual extinction ($A_V$) is derived from column density maps to calculate intrinsic colors, allowing for a reddening-independent classification.

Key Mathematical Framework

In Phase 2, to correct for the reddening effects of dust, the visual extinction ($A_V$) is calculated from the column density ($N_{H_2}$) map. The extinction in a specific band $\lambda$ is derived as:

$$ A_{\lambda} = C_{\lambda} \times A_V $$

Where $C_{\lambda}$ represents the extinction coefficient for that band (e.g., $C_J=0.29$, $C_K=0.12$). The pipeline then calculates the intrinsic colors (denoted by subscript 0) by subtracting the color excess from the measured colors:

$$ ([3.6]-[4.5])_0 = ([3.6]-[4.5])_{meas} - (A_{3.6} - A_{4.5}) $$ $$ (K-[3.6])_0 = (K-[3.6])_{meas} - (A_{K} - A_{3.6}) $$

Errors in color space are propagated using the root mean square of individual magnitude errors:

$$ \sigma_{1} = \sqrt{\sigma_{[3.6]}^2 + \sigma_{[4.5]}^2}, \quad \sigma_{2} = \sqrt{\sigma_{K}^2 + \sigma_{[3.6]}^2} $$

Final classification relies on linear cuts in the dereddened color space. For example, Class I YSOs are identified using the condition:

$$ (K-[3.6])_0 - \sigma_2 > -2.857 (([3.6]-[4.5])_0 - \sigma_1 - 0.401) + 1.7 $$

Key Results & Insights

• Contaminant Identification: The pipeline successfully identified and removed 89 PAH galaxies, 121 AGNs, and 30 shock emission sources, preventing them from mimicking YSO signatures.
• Impact of Extinction Correction: Phase 1 identified 80 Class I YSOs. However, after applying extinction corrections in Phase 2—which accounts for dust obscuration that makes stars appear redder—the count was refined to 107 Class I YSOs. This highlights the necessity of correcting for column density in dense molecular clouds.
• Population Distribution: The analysis revealed a total of 1643 non-contaminated sources. In the final extinction-corrected phase, distinct populations of Class I (enveloped protostars) and Class II (disk-bearing stars) objects were spatially isolated, allowing for the generation of region files for further astronomical analysis.